Physics of hypothermia management

The normal ‘set-point’ of core temperature is tightly regulated within the range $37\pm {0.5}^0$C, which is necessary to preserve the normal function of many enzymes and other metabolic processes. Hypothermia exists when the body’s normal thermal regulatory mechanisms are unable to maintain heat in a cold environment and core temperature falls below ${35}^0$C. Following resuscitation, the objectives of management are to rewarm the patient in a controlled manner while treating associated hypoxia (by oxygenation and ventilation if necessary), fluid and electrolyte disturbance, and cardiovascular abnormalities, particularly arrhythmias.

Heat is measured in calories. One kilocalorie is the amount of energy required to raise the temperature of $1$ L of water by $1^0$C. If an average man (weight, $75$ kg) consisted of pure water, it would take $75$ kcal to raise his temperature by $1^0$C. However, we are not made of pure water, and blood has a specific heat coefficient of $0.87$. Thus, the human body as a whole has a specific heat coefficient of $0.83$. Therefore, it actually takes $62.25$ kcal $(75\text{kg}\times 0.83)$ (round off to $62$ kcal) to raise body temperature by $1^0$C. If a patient were to lose $62$ kcal, body temperature would drop by $1^0$C. This basic thermodynamics is important in managing hypothermia.[Source: Sabiston Textbook of Surgery, 20^th edition]

Heat is transferred to and from the body by contact or conduction, air or convection, radiation, and evaporation. Conduction and radiation are the most efficient ways to transfer heat. Warming or cooling through manipulation of the temperature of IV fluids is useful as it uses conduction to transfer heat. Although IV fluids can be warmed, the U.S. Food and Drug Administration (FDA) allows fluid warmers to be set at a maximum of ${40}^0$C. So the fluid used to manage hypothermia can’t be $>{40}^0$C. $1$ L of ${40}^0$C fluid can transfer $6$ kcal heat to patient at ${34}^0$C because the temperature difference is $6^0$C. As previously noted, an average human body requires $62$ kcal to raise body temperature by $1^0$C. So to raise temperature from ${34}^0$C to ${35}^0$C, $62$ kcal is required which is provided by $\frac{62}{(40-34)}=10.3$ litres of fluid at ${40}^0$C.

Similarly if a patient were at ${35}^0$C, to raise temperature to ${36}^0$C, one needs $62$ kcal of heat which is provided by $\frac{62}{(40-35)}=12.4$ litres of fluid at ${40}^0$C.

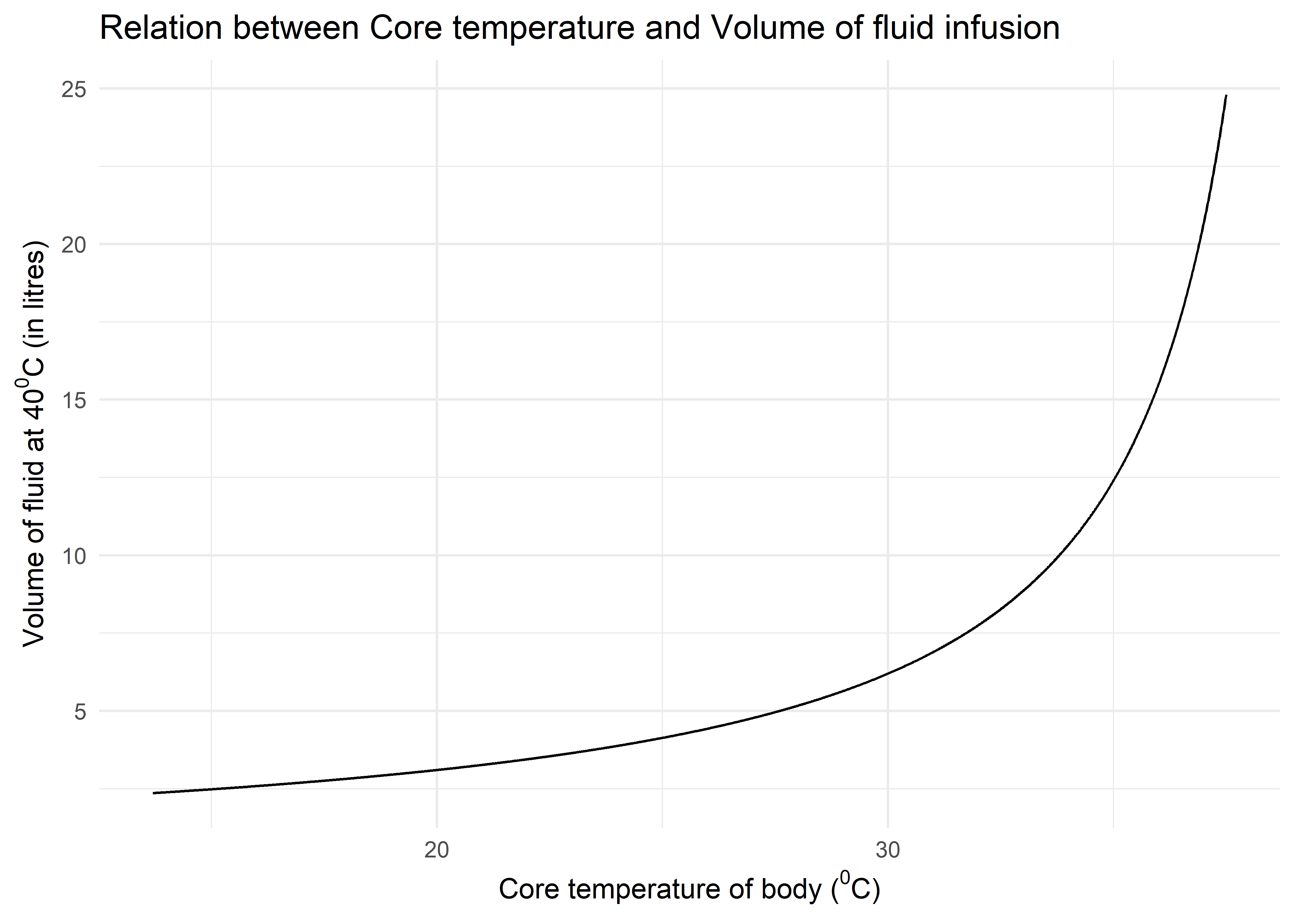
So a general pattern has emerged, the volume of litres of fluid at ${40}^0$C required to raise temperature by $1^0$C is given by equation:

$$\begin{array}{rl}& =\frac{62}{(40-\text{current temperature})}\end{array}$$

So, plotting this equation using R and ggplot2, we get the following curve. The $x$ - limit is set from ${13.7}^0$C (the lowest recorded temperature in a survivor of accidental hypothermia) to ${37.5}^0$C (normal temperature). The curve helps calculate how much volume of fluid is required to raise the temperature by $1^0$C at various physiologically possible temperatures in hypothermia.

Figure 1: Graph showing amount of fluid (in litres) required to raise temperature by 1⁰C within physiological temperature range

The curve illustrates one important fact that when temperature starts improving, more volumes of fluid is required to elevate the temperature. In practice, however, infusing so much amount of fluids is not feasible and should be combined with active and passive rewarming techniques.